Publications

On Three-Term Linear Relations for Theta Series of Positive-Definite Binary Quadratic Forms
In this paper, we investigate three-term linear relations among theta series of positive-definite integral binary quadratic forms. We extend Schiemann's methods to characterize all possible three-term linear relations among theta series of such forms, providing necessary and sufficient conditions for such relations to exist. To accomplish this, we develop, implement, and execute a novel extended refinement algorithm on polyhedral cones. We show that there is exactly one non-trivial three-term linear relation: it involves quadratic forms with discriminants −3,−12,−48, all in the same rational squareclass −3(ℚ×)2.
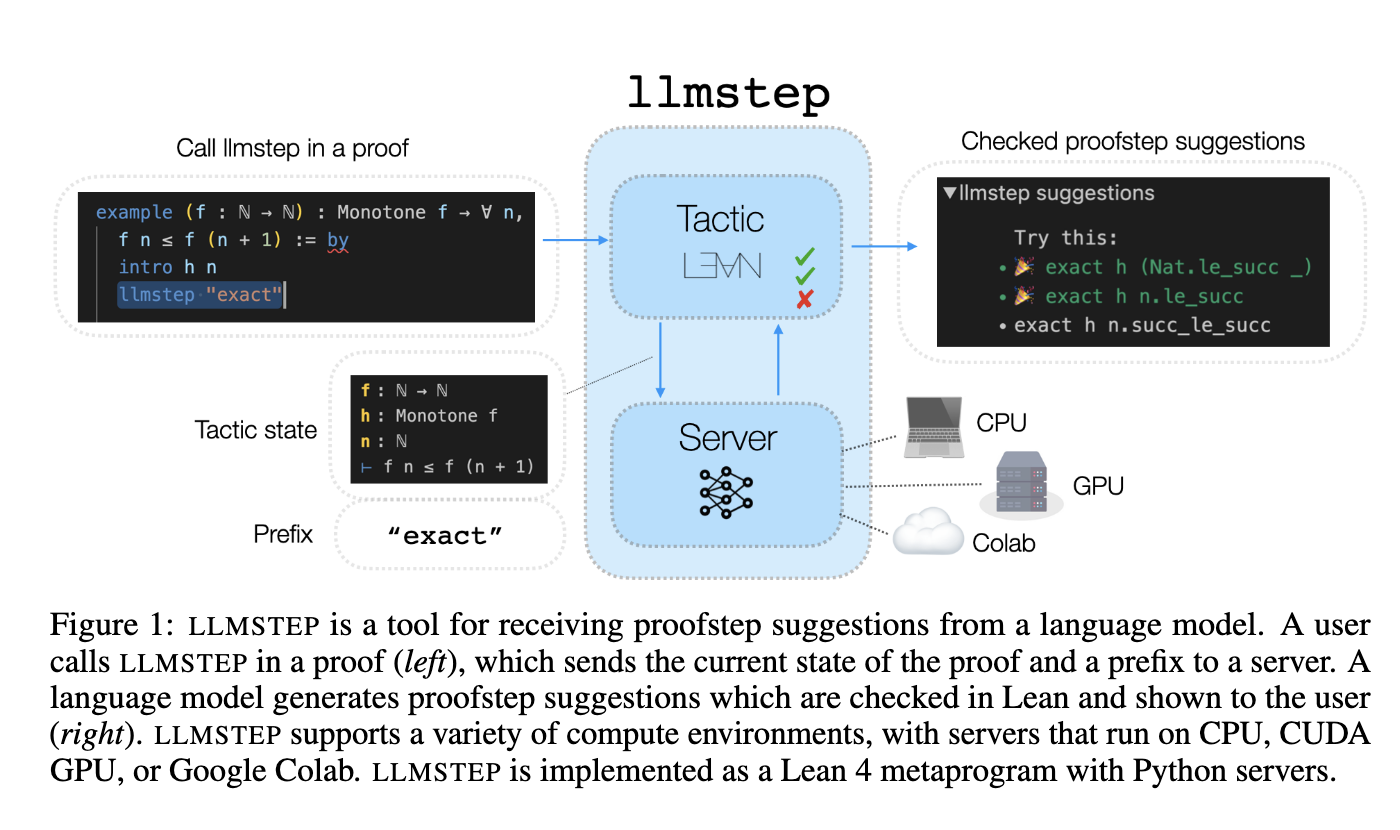
LLMSTEP: LLM Proofstep Suggestions in Lean
We present LLMSTEP, a tool for integrating a language model into the Lean proof assistant. LLMSTEP is a Lean 4 tactic that sends a user's proof state to a server hosting a language model. The language model generates suggestions, which are checked in Lean and displayed to a user in their development environment.

A New Approach Towards Autoformalization
Autoformalization is the task of automatically translating natural language mathematics into a formal language that can be verified by a program. In this paper, we propose an avenue towards tackling autoformalization for research-level mathematics, by breaking the task into easier and more approachable subtasks: unlinked formalization (formalization with unlinked definitions and theorems), entity linking (linking to the proper theorems and definitions), and finally adjusting types so it passes the type checker. In addition, we present arXiv2Formal, a benchmark dataset for unlinked formalization consisting of 50 theorems formalized for the Lean theorem prover sampled from papers on arXiv.org.

Shunno Diye Bhaag Korle Ki Hoy
This is a Q&A book written with three friends, answering some of the most frequently asked questions by both the general public as well as talented middle to high schoolers about math.
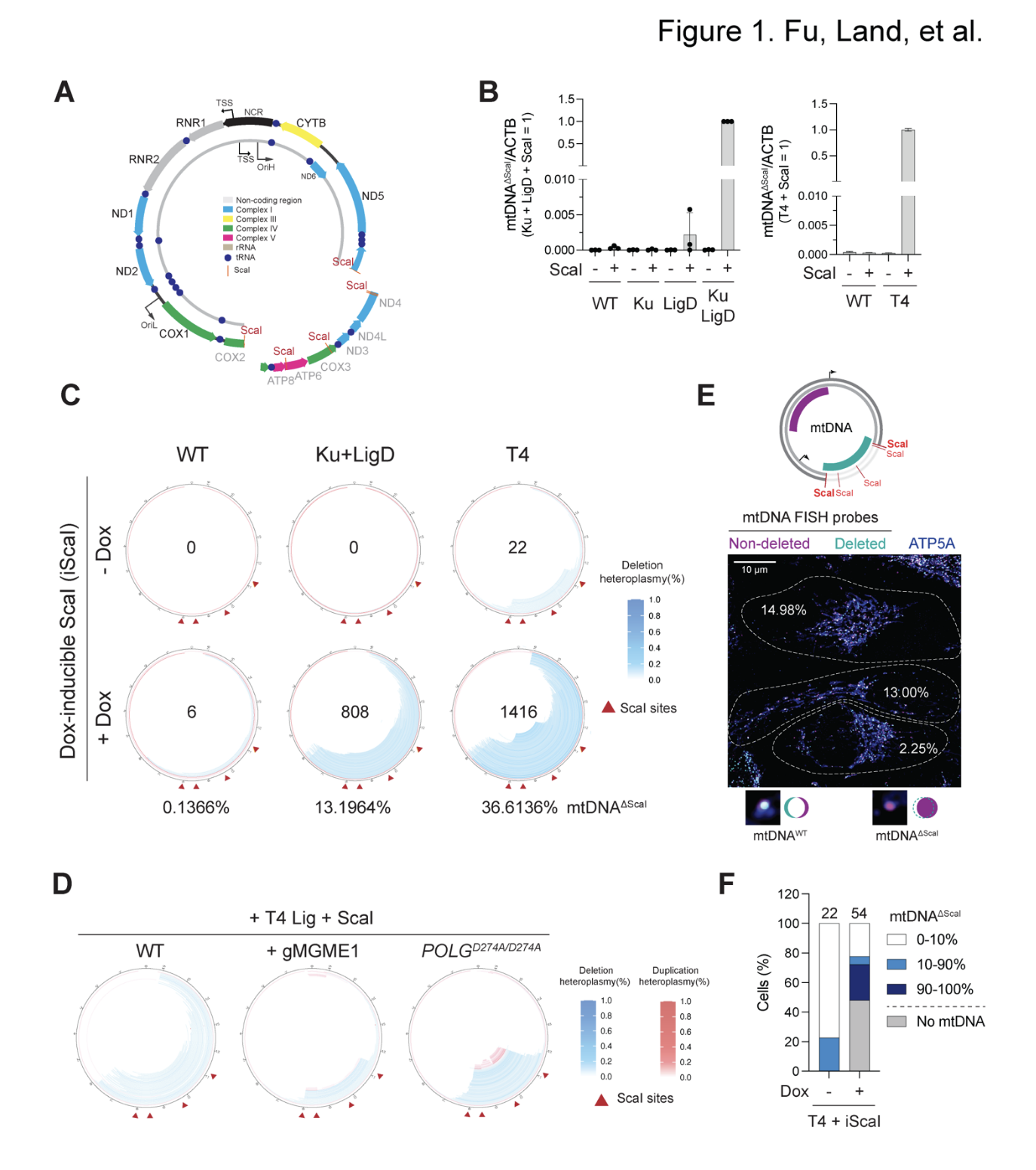
Engineering mtDNA Deletions by Reconstructing End-Joining in Human Mitochondria
Recent breakthroughs in the genetic manipulation of mitochondrial DNA (mtDNA) have enabled the precise introduction of base substitutions and the effective removal of genomes carrying harmful mutations. However, the reconstitution of mtDNA deletions responsible for severe mitochondrial myopathies and age-related diseases has not yet been achieved in human cells. Here, we developed a method to engineer specific mtDNA deletions in human cells by co- expressing end-joining (EJ) machinery and targeted endonucleases. As a proof-of-concept, we used mito-EJ and mito-ScaI to generate a panel of clonal cell lines harboring a ~3.5 kb mtDNA deletion with the full spectrum of heteroplasmy. Investigating these isogenic cells revealed a critical threshold of ~75% deleted genomes, beyond which cells exhibited depletion of OXPHOS proteins, severe metabolic disruption, and impaired growth in galactose-containing media.
